Planar ternary ring
In mathematics, a ternary ring is an algebraic structure 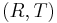 consisting of a non-empty set
consisting of a non-empty set  and a ternary mapping
and a ternary mapping 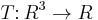 , and a planar ternary ring (PTR) or ternary field is special sort of a ternary ring used by Hall (1943) to give coordinates to projective planes. A planar ternary ring is not a ring in the traditional sense.
, and a planar ternary ring (PTR) or ternary field is special sort of a ternary ring used by Hall (1943) to give coordinates to projective planes. A planar ternary ring is not a ring in the traditional sense.
Contents |
Definition
A planar ternary ring is a structure 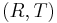 where
where  is a nonempty set, containing distinct elements called 0 and 1, and
is a nonempty set, containing distinct elements called 0 and 1, and 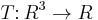 satisfies these five axioms:
satisfies these five axioms:
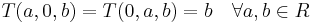 ;
;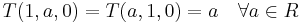 ;
;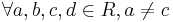 , there is a unique
, there is a unique 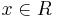 such that :
such that :  ;
;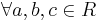 , there is a unique
, there is a unique 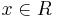 , such that
, such that 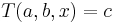 ; and
; and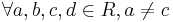 , the equations
, the equations 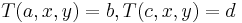 have a unique solution
have a unique solution 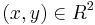 .
.
When  is finite, the third and fifth axioms are equivalent in the presence of the fourth. No other pair (0',1') in
is finite, the third and fifth axioms are equivalent in the presence of the fourth. No other pair (0',1') in 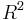 can be found such that
can be found such that  still satisfies the first two axioms.
still satisfies the first two axioms.
Binary operations
Addition
Define 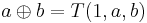 . The structure
. The structure 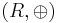 turns out be a loop with identity element 0.
turns out be a loop with identity element 0.
Multiplication
Define 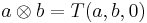 . The set
. The set 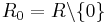 turns out be closed under this multiplication. The structure
turns out be closed under this multiplication. The structure 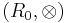 also turns out to be a loop with identity element 1.
also turns out to be a loop with identity element 1.
Linear PTR
A planar ternary ring 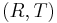 is said to be linear if
is said to be linear if 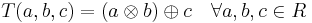 . For example, the planar ternary ring associated to a quasifield is (by construction) linear.
. For example, the planar ternary ring associated to a quasifield is (by construction) linear.
Connection with projective planes
Given a planar ternary ring 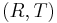 , one can construct a projective plane in this way (
, one can construct a projective plane in this way (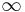 is a random symbol not in
is a random symbol not in  ):
):

![B=\{[a,b]|a,b \in R\}\cup\{[a]|a \in R \}\cup \{[\infty]\}](/2012-wikipedia_en_all_nopic_01_2012/I/c2c09860adb0206229e680e9faf5b0cf.png)
- We define the incidence relation
 in this way (
in this way (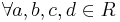 ):
):
One can prove that every projective plane is constructed in this way starting with a certain planar ternary ring. However, two nonisomorphic planar ternary rings can lead to the construction of isomorphic projective planes.
References
- Albert, A. Adrian; Sandler, Reuben (1968). An Introduction to Finite Projective Planes. New York: Holt, Rinehart and Winston.
- Hall, Marshall (1943), "Projective planes", Transactions of the American Mathematical Society (American Mathematical Society) 54 (2): 229–277, ISSN 0002-9947, JSTOR 1990331, MR0008892
![((a,b),[c,d])\in I \Longleftrightarrow T(c,a,b)=d](/2012-wikipedia_en_all_nopic_01_2012/I/0cc2b05add45da264990a7b3bd207c70.png)
![((a,b),[c])\in I \Longleftrightarrow a=c](/2012-wikipedia_en_all_nopic_01_2012/I/9de9b4a17e55c7ca5efbad76206839a8.png)
![((a,b),[\infty])\notin I](/2012-wikipedia_en_all_nopic_01_2012/I/ae53fb4af48749dd76a390568d19df4b.png)
![((a), [c,d])\in I \Longleftrightarrow a=c](/2012-wikipedia_en_all_nopic_01_2012/I/95f186faa28bde1ae07426d1e5850a41.png)
![((a), [c])\notin I](/2012-wikipedia_en_all_nopic_01_2012/I/28da84db95499c50f6e9c1e82d03384c.png)
![((a),[\infty])\in I](/2012-wikipedia_en_all_nopic_01_2012/I/e61b295ffae96c2e02f944cf7dea03ea.png)
![(((\infty),[c,d])\notin I](/2012-wikipedia_en_all_nopic_01_2012/I/9c62a7566843822ece9b7e61dd0a390a.png)
![((\infty),[a])\in I](/2012-wikipedia_en_all_nopic_01_2012/I/a9d7a9e008c2fb1e8ec8e2631b69c143.png)
![((\infty),[\infty])\in I](/2012-wikipedia_en_all_nopic_01_2012/I/85b517722453203794164c609ee959be.png)